LA REPRESENTATION
EN PERSPECTIVE
OBLIQUE
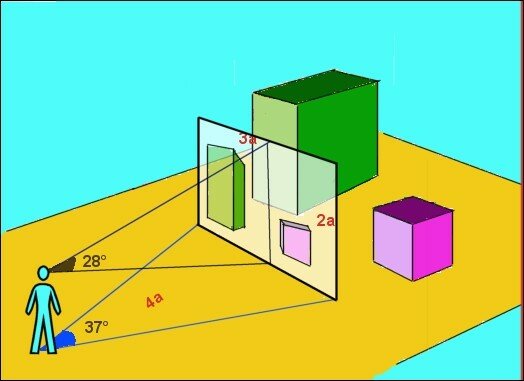
Notre perception visuelle.

Notre vision nette est la
base
d’une pyramide ayant un angle de 37° sur le plan horizontal et 28° sur
le plan
vertical.
Pour voir dans son
intégralité un
objet de 4m de large ou de 3m de hauteur, l’observateur doit se situer
à 6m de
l’objet.
PASSAGE
DE LA PERSPECTIVE FRONTALE A LA PERSPECTIVE
OBLIQUE
Si l’observateur se déplace parallèlement au tableau, la vue des face se trouve modifiée.
SI ON TIENT COMPTE DE LA PYRAMIDE OPTIQUE (angle de 37°), lorsqu’il est placé au point de vue n°3, il ne perçoit pratiquement plus le volume vert et il perçoit la face droite du volume violet.
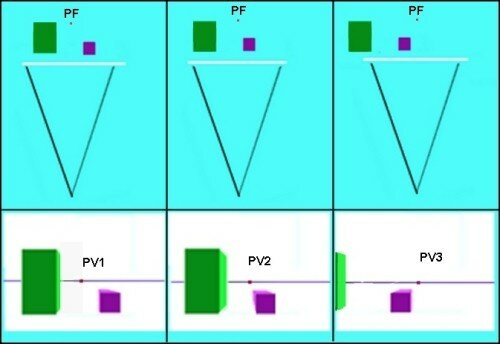
S’il avance encore vers la droite, le volume vert disparaît.

Les
arêtes verticales conservent leur propriété.
Les arêtes de chaque face latérale convergent vers un
point de fuite situé sur la ligne d’horizon, chaque face déterminant un
point
de fuite.
Voici l'observation en perspective oblique d'un volume (plus grand que l'observateur.
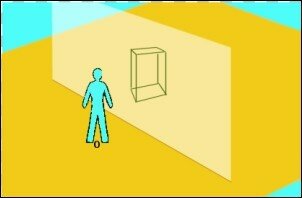
Réalisons le dessin en tenant compte de la distance de l'observateur.
Réalisons le dessin en
partant de notre connaissance de la représentation en
perspective frontale.
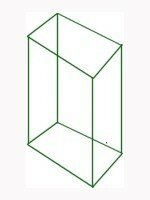
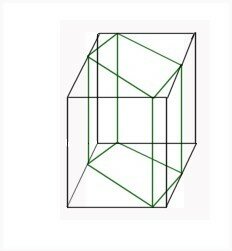
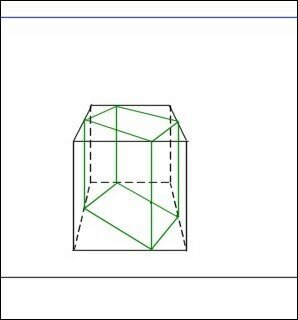
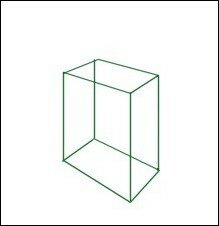
Voici une vue du volume en perspective cavalière :
|
|
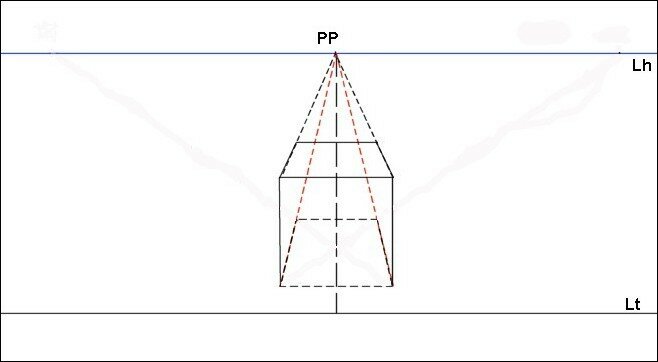
Il est contenu dans un volume présentant une face frontale que nous savons dessiner. Les arêtes horizontales non parallèles à la ligne de terre se rejoignent au point de fuite PP de la ligne d’horizon.
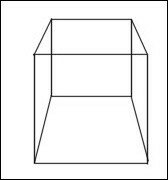
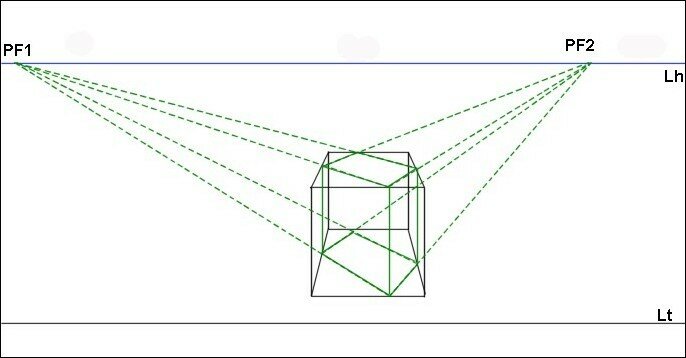
Les
4 arêtes verticales du volume
vert touchent bien les 4 faces du volume qui le contient.
Ce dessin, approximatif, répond
aux particularités du volume que nous voulons représenter.
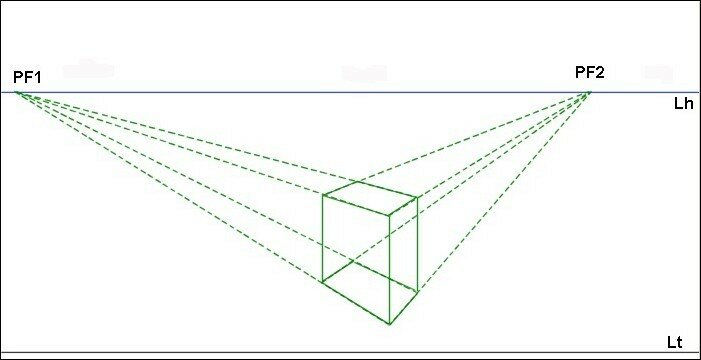
Nous constatons que les arêtes
horizontales se rejoignent sur la
ligne
d’horizon en 2 points de fuite conformément à nos observations sur les
points
de fuite des parallèles horizontales.
|
|
Nous allons refaire cette construction avec plus de précision, en partant de la vue de dessus :
(Plusieurs solutions possibles)
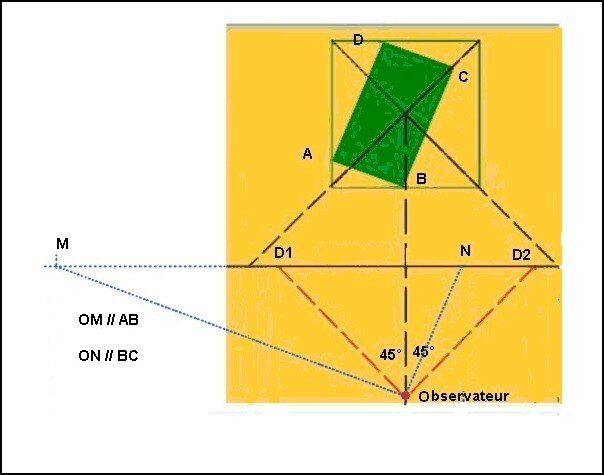
Notre
volume de base ABCD est contenu dans un
cube (base carrée) dont une face est parallèle au tableau.
On note sur la ligne de terre les 2 points de
distance D1 et D2 .
On trace OM parallèle à AB et ON parallèle à BC
de manière à connaître la position des points de fuites des arêtes
horizontales.
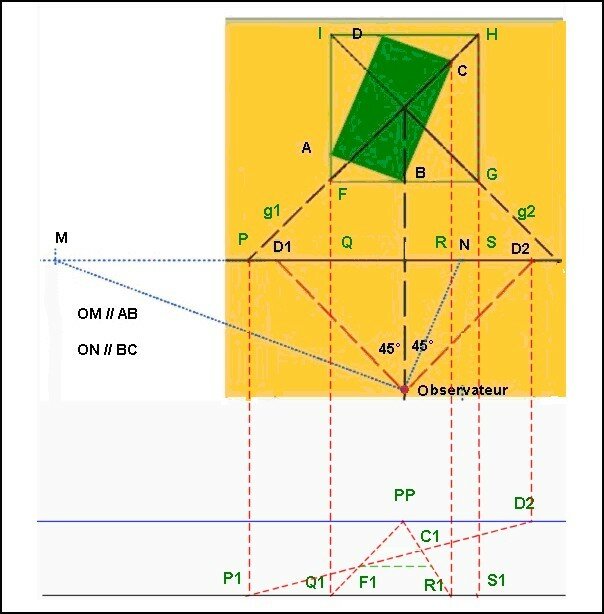
Traçons P1D2 , droite qui
représente g1 ,
diagonale du carré.
Traçons Q1PP sur laquelle se situe représentation du segment FI ; on
trouve donc F1
Traçons R1PP sur laquelle se situe la représentation du point C ; on
trouve donc C1
Le point représentant B est situé sur la parallèle à la ligne de terre
menée
par F1
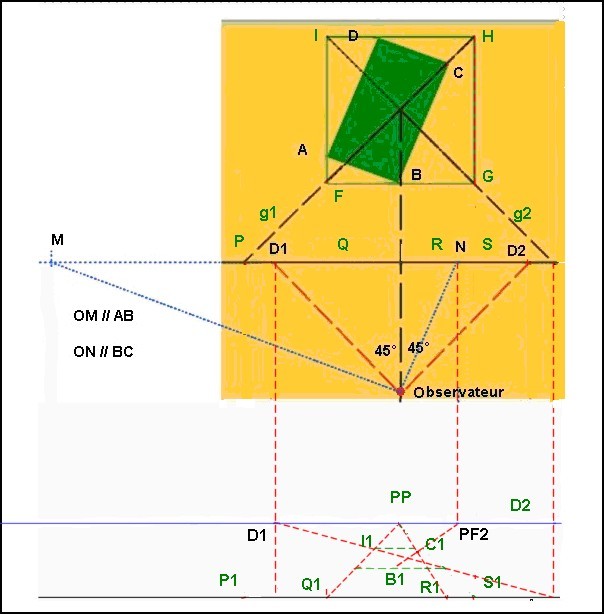
![]()
Traçons C1PF2
pour déterminer le
point B1.
Nous traçons ensuite par D1 la représentation de la diagonale g2 qui
nous permet de noter I1 et la
représentation de l’arête IH sur laquelle de trouve D
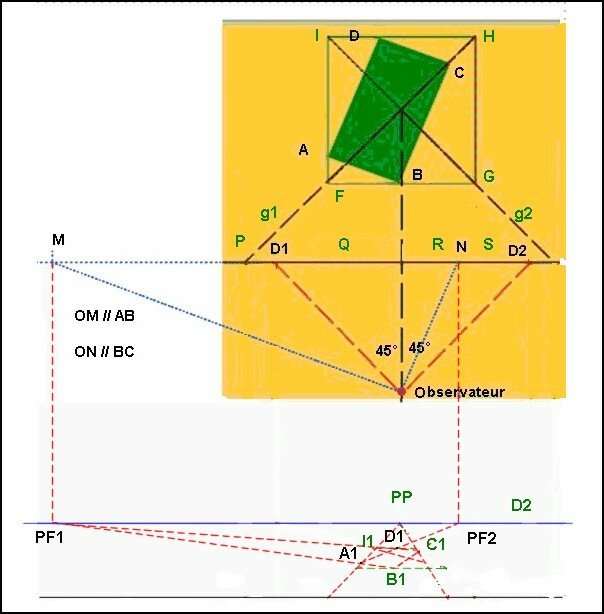
![]()
En
utilisant le point de fuite PF1 nous
déterminons A1
En utilisant le point de fuite PF2 nous
déterminons D1
Nous pouvons donc tracer la base A1B1C1D1 du
volume.
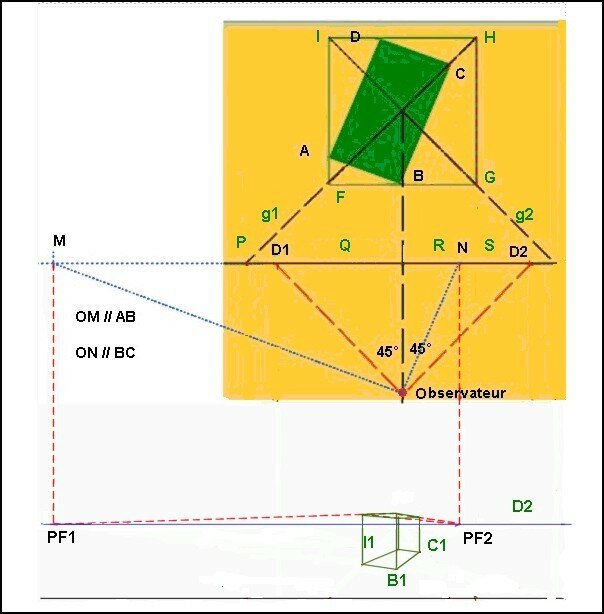
Traçons un premier segment vertical par B1 (de longueur arbitraire par absence de donnée !)
Le tracé des lignes de fuite et des arêtes verticales permet d’achever la construction du volume.
UN NOUVEAU POINT DE VUE...
Nous supposons que l’observateur s'est déplacé…
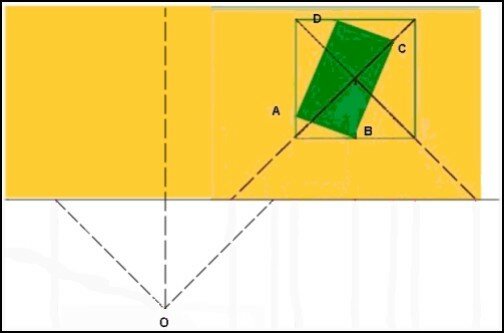
Quelle vue aura-t-il du volume ?
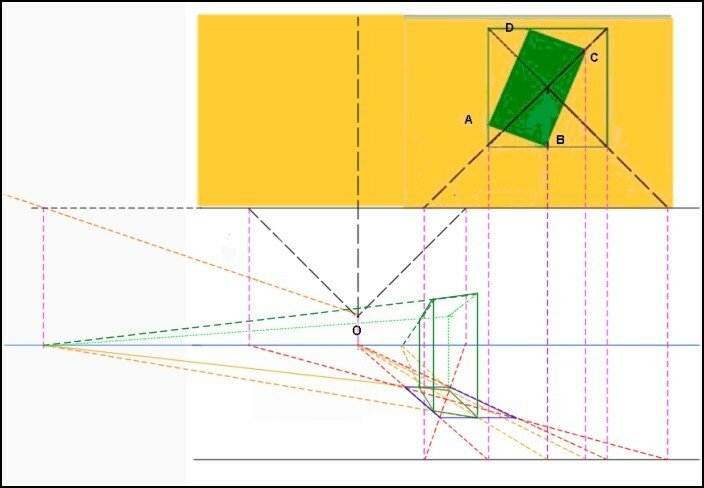
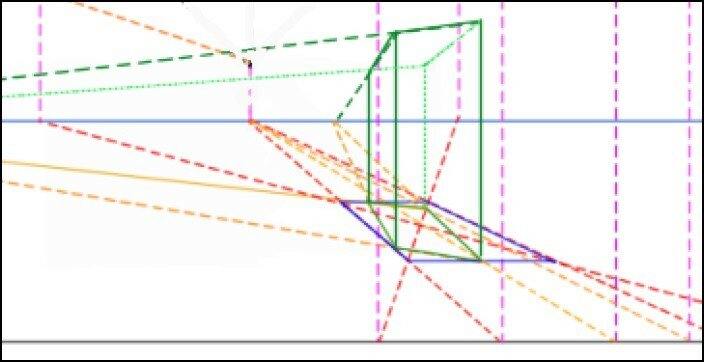
Dans la pratique, le peintre ne fera certainement pas de telles constructions !
L’essentiel sera d’estimer l’emplacement des points de fuite afin de tracer au mieux les arêtes du volume observé.
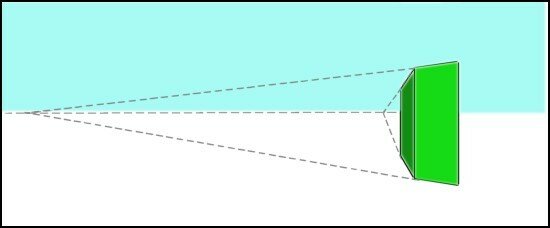
IV.1 Dessiner en perspective oblique ces deux volumes.
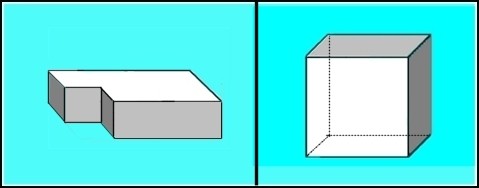
Dans un dessin
en perspective OBLIQUE, -
Chaque objet a,
au premier plan, une arête parallèle au plan du dessin - Toutes les verticales conservent leur propriété sur le dessin - Toutes les lignes fuyantes convergent sur la ligne d’horizon vers deux points de fuite. |
PROBLEME : LA DIVISION DES PLANS FUYANTS

Je sais comment ajuster la hauteur des arbres le long de la
route. Mais comment déterminer leur emplacement ?
Comment diviser le plan vertical fuyant en parties égales ?
(Revoir éventuellement la partie relative aux points de distance)
Nous allons diviser un plan fuyant en 3 parties égales.
PREMIÈRE SOLUTION
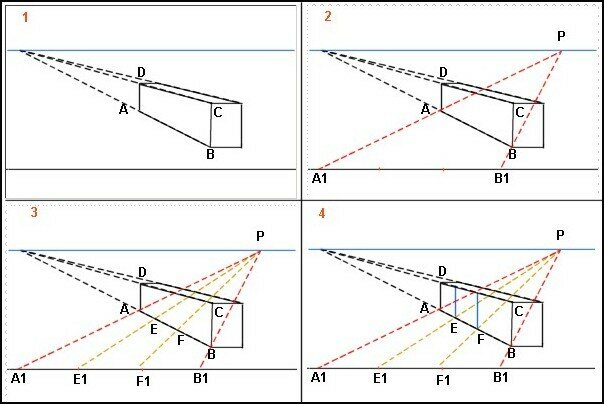
2. A partir d’un point P de la ligne d’horizon, nous projetons sur la ligne de terre les extrémités A et B de la partie à diviser. A1B1 est divisé en trois segments égaux.
3. PA1 PE1 PF1 PB1 étant des parallèles E et F divisent AB en trois segments égaux.
4. Il suffit de tracer les verticales en E et F.
SECONDE SOLUTION
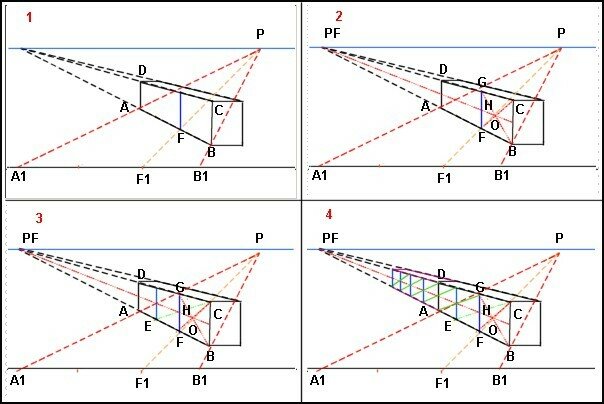
1 . Comme précédemment, nous cherchons le premier point tel que FB= 1/3 AB
2. O est l’intersection des diagonales de BCGF. Nous traçons CPF.
3. CH coupe AB en E. BF=FE
Le plan vertical est bien divisé en 3 parties égales.
4. L’avantage de cette solution est de se dispenser de noter tous les points de la ligne de terre (ce qui dépasserait le cadre de la feuille !)
En
répétant les tracés, on peut
continuer à
diviser le plan fuyant…
Compléter
les
dessins suivants
(utiliser la
solution de votre choix).
V.1

VI.2
VI.3

Attention à
l’emplacement du pied du second
lampadaire… !!
VI.4 Voici un bâtiment en perspective oblique. Il a 2 étages garnis de baies vitrées. Au rez-de-chaussée des devantures…
Compléter le dessin
VI.5 Voici
une jolie photo-montage .Hélas, bien ratée.
Trouvez l’erreur. Vous pouvez aussi refaire
le dessin.
